Recently I have spent some time learning and playing with Generative Adversarial Networks (GANS). In this article I provide a brief introduction into what a GAN is, and present a GAN that I built to generate numerical images similar to those found in the MNIST database.
What is a GAN?
GAN’s are a relatively new neural network model, introduced by Ian Goodfellow in 2014 [1]. There are two major components (models) to a GAN, a generator and a discriminator. The generator is a model that takes random noise as an input and uses that data to generate an output item (often an image). The discriminator is another model that takes items from two sources; output from the generator, and ground truth data. The objective of the discriminator is to identify whether the provided input data is genuine or fake (in a sense, the discriminator is acting as a forgery detector).
These two models are repeatedly trained, one after the other. Conceptually, training and improving the discriminator encourages a performance improvement from the generator, which is trying to trick the discriminator. Then, training the generator (ideally) results in more realistic output data, making it harder to tell the difference between genuine and fake (generator) data, which in turn encourages an improvement in performance of the discriminator. The back and forth training process allows for the two models to help each other improve.
Getting GANs to work is often easier said than done, with a lot of tricks implemented to improve the chances of producing a successful model (link). There are also several types of GANs, with a list of them here for the interested reader. Some interesting examples of what GANs can do can be seen at the following links (refresh to see new examples):
- This person does not exist
- This airbnb does not exist
- These cats do not exist
- This waifu does not exist
My Model
To get a better understanding of GANs and how they work, I built a Deep Convolutional GAN (DCGAN) with the objective of training a model to generate numerical images. The ground truth labels that I would be trying to reproduce were the MNIST numbers. I chose to build a DCGAN over something simpler (such as a GAN with a handful of dense layers) as I wanted to give my GPU’s a little more work to do.
Before we dive into a explanation of my model, I would like to reference and acknowledge Naoki Shibuya for providing a strong introduction article that accelerated my understanding of how to build a GAN. While my model is different to that of Naoki, it is similar to a lot of other models presented by others (such as this or this). There is a lot of tuning that goes into a GAN, and using the work of others for inspiration helped to save me a lot of headache.
Focusing on the model that I built, we first import everything needed to train the model. I built a model using the Keras package wrapped around a GPU variant of TensorFlow.
import keras
from keras.models import Sequential
from keras.layers import Dense, Activation, BatchNormalization, Reshape, UpSampling2D, \
Conv2D, MaxPooling2D, Flatten
from keras.optimizers import Adam, SGD
import numpy as np
import matplotlib.pyplot as pltWith everything imported, I then define my generator. The first layer is a Dense one, and is included to add some relationship between the input data (which is I.I.D. noise). From here, the data is reshaped and passed through a series of Conv2D layers, which are used to learn image-based features.
def model_generator():
model = Sequential()
model.add(Dense(input_dim=100, units=1024))
model.add(Activation('tanh'))
model.add(Dense(128*7*7))
model.add(BatchNormalization())
model.add(Activation('tanh'))
model.add(Reshape((7, 7, 128), input_shape=(128*7*7,)))
model.add(UpSampling2D(size=(2, 2)))
model.add(Conv2D(64, (5, 5), padding='same'))
model.add(Activation('tanh'))
model.add(UpSampling2D(size=(2, 2)))
model.add(Conv2D(1, (5, 5), padding='same'))
model.add(Activation('tanh'))
return modelWith the generator function defined, the discriminator is now defined. The model is a combination of simple MaxPooling and Dense layers with a single Conv2D layer as shown below. The final output of this model is a single node that describes the models belief as to whether the input image was genuine (1) or fake (0). The final activation layer is a sigmoid curve to give us this probabilistic estimate.
def model_discriminator():
model = Sequential()
model.add(
Conv2D(64, (5, 5),
padding='same',
input_shape=(28, 28, 1)))
model.add(Activation('tanh'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(128, (5, 5)))
model.add(Activation('tanh'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(1024))
model.add(Activation('tanh'))
model.add(Dense(1))
model.add(Activation('sigmoid'))
return modelWith the two sub-models defined, we now import and define the training and test data (in this description I haven’t used the test data, though we could pass it through the trained discriminator to understand its performance.). Because we are using tanh activation layers, the training data is transformed so that its range lies between [-1,1] (based on tricks listed here).
(X_train, y_train), (X_test, y_test) = keras.datasets.mnist.load_data()
X_train = (X_train / 255 - 0.5) * 2 #Want to change from 0-255 to -1,1
#Add dimensions for passing into models (saves a data.reshape() later)
X_train = X_train[:, :, :, None]
X_test = X_test[:, :, :, None]We can look at a sample of ‘true’ images of hand-drawn numbers. We can compare these to the images from a trained generator model.
plt.figure(figsize=(10, 8))
for i in range(20):
img = X_train[i,:,:,0]
plt.subplot(4, 5, i+1)
plt.imshow(img, cmap='gray')
plt.xticks([])
plt.yticks([])
plt.tight_layout()
plt.show()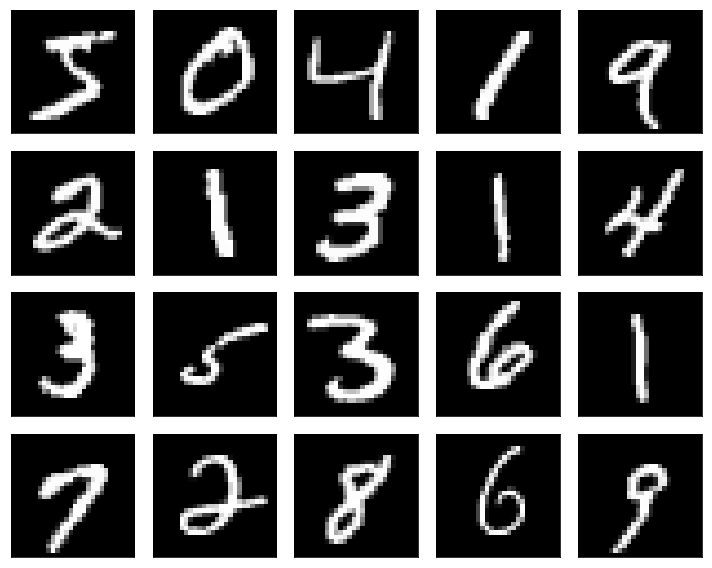
We now instantiate a generator and discriminator model, and combine them to form the GAN model. The discriminator training is set to false initially so that we can start by training the generator model.
gen = model_generator()
disc = model_discriminator()
gan = Sequential()
gan.add(gen)
disc.trainable = False
gan.add(disc)With the models setup, we now define the learning functions and rates for both the discriminator and generator. Note that the choice of which learning function to use, and what learning rate to use, both have an influence on how successful the final model will be.
d_optim = SGD(lr=0.0005, momentum=0.9, nesterov=True)
g_optim = SGD(lr=0.0005, momentum=0.9, nesterov=True)
# d_optim = Adam(lr=0.0005)
# g_optim = Adam(lr=0.0005)
gen.compile(loss='binary_crossentropy', optimizer="SGD")
gan.compile(loss='binary_crossentropy', optimizer=g_optim)
disc.trainable = True
disc.compile(loss='binary_crossentropy', optimizer=d_optim)From here, we can now train the model! Again, the choice of some variables here such as BATCH_SIZE and noise. The largest choice to make with the noise data, is whether it is sampled from a normal or uniform distribution. I have explored both (and both work), though in this instance I present results from noise sampled from a normal distribution. The discriminator training is toggled (freezing and unfreezing its weights) when training the generator. This is done so that we can alternatively train the two models as mentioned above.
Note that one thing that could definitely be done here would be to look into some metric for determining when to stop training the model, and to also potentially look at a decaying learning rate over time. To keep things simple, I just trained the model for 100 interations.
BATCH_SIZE = 64
for epoch in range(100):
print("Epoch:", epoch)
for index in range(int(X_train.shape[0]/BATCH_SIZE)):
#noise = np.random.uniform(-1, 1, size=(BATCH_SIZE, 100))
noise = np.random.normal(0, 0.3, size=(BATCH_SIZE, 100))
X_batch = X_train[index*BATCH_SIZE:(index+1)*BATCH_SIZE]
generated_images = gen.predict(noise)
X = np.concatenate((X_batch, generated_images))
y = [1] * BATCH_SIZE + [0] * BATCH_SIZE
d_loss = disc.train_on_batch(X, y)
#noise = np.random.uniform(-1, 1, (BATCH_SIZE, 100)
noise = np.random.normal(0, 0.3, size=(BATCH_SIZE, 100))
disc.trainable = False
g_loss = gan.train_on_batch(noise, [1] * BATCH_SIZE)
disc.trainable = True
print('d_loss : %f' % (d_loss))
print('g_loss : %f' % (g_loss))With the model trained, we can now see what the generated images look like. To do this, we sample 20 images and present them below (note that I ran this a few times to get a set of images I liked). We can see that most of the numbers generated from my model look reasonable, even to the point where I would not be able to identify them as being fake. However, there are also some numbers that look questionable. Overall though, I think the model is performing well, especially for a first GAN model.
noise = np.random.normal(0, 0.3, size=(20, 100))
generated_images = gen.predict(noise)
plt.figure(figsize=(10, 8))
for i in range(20):
img = generated_images[i,:,:,0]
plt.subplot(4, 5, i+1)
plt.imshow(img, cmap='gray')
plt.xticks([])
plt.yticks([])
plt.tight_layout()
plt.show()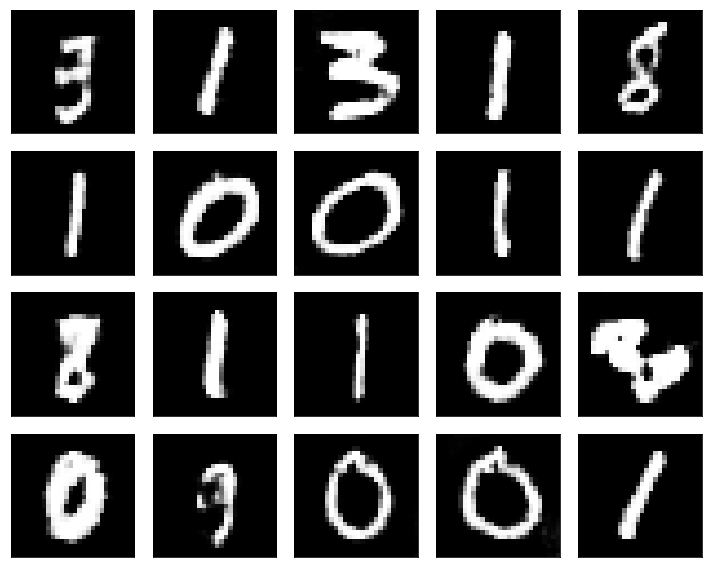
Discussion and Conclusion
In this post, I have developed a simple DCGAN model to generate images of numerical digits. Example images generated from the resulting model are presented above, and several of these images look realistic, though there are a few obviously wrong images.
In the samples presented, there are also a lot of generated 0’s and 1’s. I believe that these occur the most as they are the most general shapes and therefore the easiest to learn. This means that these images are the easiest to trick the discriminator into classifying as true. It is possible that further training would allow for more detailed features to be learned, allowing for more complex numbers like 8 to be ‘drawn’ better.
Finally, it is also worth noting that more than almost three quarters of the generated images are either 0 or 1. Part of this is likely due to the strength of the model in generating these shapes. However, the more noteworthy aspect is that the objective of the generator model is only to produce numerical images that trick the generator, not to produce a balanced sample of all images.
I hope that this post has provided some insight into GANs, their strengths, and how such a model might be developed. Thanks for reading!
References
[1] Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., & Bengio, Y. (2014) Generative adversarial nets. In Advances in neural information processing systems (pp. 2672-2680).